What Is Directivity Function?


Directivity function (DF) of a ground based particle detector is a function D(A,B) of asymptotic longitude A and asymptotic latitude B. It defines the contribution of primary protons, arriving from a given asymptotic direction (A,B) to the count rate of the detector, so it describes directional sensitivity of the detector to primary protons. When integrating D(A,B) over A and B, the count rate of a monitor is obtained. The DF enables one to determine the acceptance cone, inside which the coming protons contribute to a given percentage of the count rate. Thus the DF is an inseparable characteristic of ground based particle detectors – muon and neutron monitors.
What is the shape of Directivity Function?
The count rate of a monitor is created by the flux of secondary particles falling on the monitor inside a vertical cone. These secondary particles are created by the primary particles (protons and alpha particles). The directions of primary and secondary particles are close each to other. If the Earth had no magnetic field, it would be possible to continue the cone to infinity and achieve a solid angle within which the entering primary particles are responsible for creating the count rate of monitor. In this case the asymptotic directions of primary particles approximately coincide with the falling directions of secondary particles, therefore the DF would be some circular function, shown in the left panel of Fig.1. However Earth’s magnetic field strongly deflects the trajectories of primary particles in magnetosphere, causing the asymptotic directions to differ significantly from the falling directions. As a result a non trivial shape of the DF, shifted to east, is formed, shown in the right panel of Fig.1.
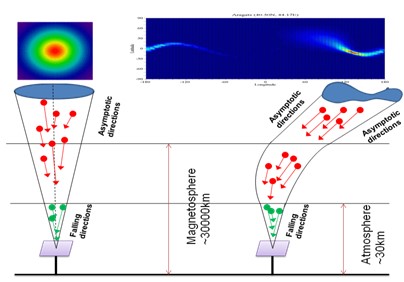
Fig.1 Sketch of directivity function of a particle detector (right panel), and in the assumption of the absent of Earth magnetic field (left panel) in arbitrary scale. Red and green arrows are correspondingly primary protons and secondary neutrons.
The shape of DF depends significantly on location of NM station. The acceptance cones of NMs, located at low and middle latitudes, are significantly wider than those of NM located at high latitudes. Herewith, the cross sections of acceptance cones of NMs, located at positive latitudes, are upward curved (Aragats, Athens, Mexico…), whereas the cross sections of acceptance cones of other NMs, located at negative latitudes (Hermanus, LARC, Kingstone,…) are downward curved.
How directional sensitivity of an NM was determined in the past?
Directional sensitivity of a NM was determined by asymptotic direction of primary protons with median energy, vertically falling on the atmosphere, assuming that it is the direction of maximum sensitivity of a NM (the direction of acceptance cone). However this approach does not clarify how much this direction deflects from exact direction of maximum sensitivity, as well as what is the width of acceptance cone, i.e. what is directional resolution of a NM. The DF enable to obtain exact direction of maximum sensitivity of a NM and the width of acceptance cone. It clarifies directional resolution of the NMs, located at different latitudes, showing that higher latitude NM predominantly has narrower acceptance cones (which was known in the past qualitatively).
How is Directivity Function Computed
To derive the DF it is necessary to calculate many asymptotic directions, corresponding to primary protons having rigidities from the cutoff rigidity to about 200GV, and falling on the atmosphere along different directions inside a ~ 60o vertical cone. Asymptotic directions are computed by using the PLANETOCOSMICS code with tilted dipole model of Earth magnetic field. We use the 3o step size of zenith angle (q = 3o, 6o,…60o) and 3o/sin(q) step size of polar angle, which leads to 1212 falling directions evenly filling the 60o cone. Each direction corresponds to a dot in geographic coordinates. The dots are binned according to their asymptotic longitude A and latitude B with weight coefficients, accounting differential spectrum of primary protons. As a result a function F(A,B) is obtained, which describes the distribution of primary protons, falling on the atmosphere inside a 60o vertical cone by their asymptotic directions. Next, it is necessary to use the yield function of neutron monitor to connect count rate of NM with F(A,B), and thus, to convert F(A,B) to sought directivity function D(A,B).
The database of Directivity Function
The database contains Directivity Functions of 39 NM stations, located at low, middle and high latitudes. Directivity Functions are presented in geographic coordinates in the interval of longitudes (–180o…180o) and in the interval of the latitudes (–90o…90o). We compute the discrete values of D(A,B) with the step size 5o, and obtain a 72 x 36 matrix. These values are plotted as a 2D color coding graph by using MatLab. The color-coding gives the flux of primary galactic protons from blue (no contribution) to red (maximum contribution). E.g. the DF of Aragats NM is presented in Fig.2. It can be seen that DF reaches its maximum values in vicinity of asymptotic direction A ~ 130o and B ~ –10o. Note that the vertical direction is determined by the coordinate of the NM station, that is Aver ~ 44o and Bver ~ 40o. Thus, the direction of the maximum sensitivity of Aragats NM largely deflects from the vertical direction.
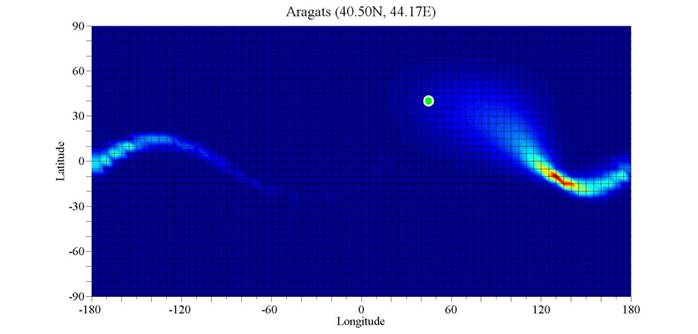
Fig.2 Directivity Function D(A,B) of Aragats NM. The color-coding gives the flux of primary galactic protons from blue (no contribution) to red (maximum contribution). Open circle shows Aragats location (40.5N, 44.17E)
Glossary
Asymptotic direction
asymptotic direction of a particle that falls on the atmosphere at given polar and zenith angles, is the direction from which this particle enters the magnetosphere
Acceptance cone
“the acceptance cone is the solid angle containing the asymptotic directions of primary protons that significantly contribute to the counting rate of the detector“ (McCracken, K.G., J. Geophys. Res., 67, 423, 1962, McCracken, K.G., Rao, U.R., Ness, N.F., J. Geophys. Res., 73, 4159, 1968)
Cuttoff rigidity
The minimal rigidity, required for a primary proton to reach a given position at the top of the atmosphere
Median energy of primary protons the energy, above which the primary protons contribute about 50% to the NM count rate.
Yield function Y(R,q) gives the number of count of a NM, produced by a primary proton, having rigidity R and falling on the atmosphere at zenith angle q.
